Technology has been evolving for years now and we are at a stage where you can find a solution to almost every problem with the help of technology. But, what about the times when not much was known about advanced technology to the humankind.
There were problematic situations that needed a smarter solution with the minimum technical sources. It was back then that Monte Carlo simulation was introduced. It is a technique based on probability to reduce the risk of the outcome of decision-makers in problematic areas like events, such as a game at the casino.
This blog discusses the concept of Monte Carlo simulation, its history, its use and purpose, how it helps in career and a few examples to support the subject.
Monte Carlo Simulation
Monte Carlo Simulation, also called the Monte Carlo Method, is a kind of computer simulation technique that works on probability distributions of the most possible outcome of a decision to be made. By constructing the probability distributions of the possible outcomes, you are allowed to assess the level of risk quantitatively and take a particular decision based on the result (risk involved). This way, you get the perfect balance of benefit against risk in the division you choose to make.
Monte Carlo simulation has been used for years and is applicable in different streams such as finance, engineering, mathematics, data science, and various other business applications.
History of Monte Carlo Simulation
Monte Carlo simulation or Monte Carlo method was named after Monaco, a city known for its casino and game of chance, such as roulette included repetitive events with known probabilities. The concept remained veiled under its undeveloped applications during the earlier years of its introduction. It was in 1940s that the modern application of Monte Carlo simulation was fairly introduced. It was the time when atomic bomb work was the concern.
A mathematician, Stanislaw Ulam was the one to recognize the way how computers could make Monte Carlo method for complex systems possible. He said:
“The first thoughts and attempts I made to practice [the Monte Carlo Method] were suggested by a question that occurred to me in 1946 as I was convalescing from an illness and playing solitaires. The question was what are the chances that a Canfield solitaire laid out with 52 cards will come out successfully? After spending a lot of time trying to estimate them by pure combinatorial calculations, I wondered whether a more practical method than “abstract thinking” might not be to lay it out say one hundred times and simply observe and count the number of successful plays. This was already possible to envisage with the beginning of the new era of fast computers, and I immediately thought of problems of neutron diffusion and other questions of mathematical physics, and more generally how to change processes described by certain differential equations into an equivalent form interpretable as a succession of random operations. Later … [in 1946, I] described the idea to John von Neumann, and we began to plan actual calculations. Eckhardt, Roger (1987).”
- Stan Ulam, John von Neumann, and the Monte Carlo method, Los Alamos Science, Special Issue (15), 131-137
The core idea of the Monte Carlo method is to use random samples of inputs or parameters to understand the behavior of a complex process or system. It came into use for the scientists working on the atomic bomb. They encountered a physics problem, such as the models of neutron diffusion, that was complicated to solve analytically. And, there was a need for finding a numerical solution.
Thankfully, the scientists had access to one of the first models of computers, Maniac. But, the models they designed included so many dimensions that numerical evaluation was slow and exhaustive. Monte Carlo simulation proved to be effective in solving these complex problems. This is how the Monte Carlo method became popular over time and is now used in various diverse range of problems – from science to finance to different business applications.
Need to use Monte Carlo simulation
How do you manage a work that includes a forecast, estimate or make a decision where there is major uncertainty? This is when you will be advised to use the Monte Carlo simulation. The need to use the Monte Carlo method is that to make sure your forecasts or estimates are not off the mark, leading to negative consequences for your decisions.
A noted individual, well-versed with simulation and other similar methods, says “Many people, when faced with an uncertainty … succumb to the temptation of replacing the uncertain number in question with a single average value. I call this the flaw of averages, and it is a fallacy as fundamental as the belief that the earth is flat.”
Similar to the physics problem during the 1940s, there are several business activities, processes and plans that are too complex to be solved analytically. Thankfully, you can create a spreadsheet model that allows you to solve the issue numerically. In the process, you can use numbers, consider ‘what ifs’ and see the outcomes. It is a straightforward process when you have only a couple of parameters in consideration.
But, there are some business situations that involve a lot of uncertainties in costs or other factors. If you come across a situation like this, you need to use the Monte Carlo simulation for successful results.
Requirements for using Monte Carlo simulation
In case you want to use the Monte Carlo method or Monte Carlo simulation, you need to build a quantitative model of your business plan, activity or process. One of the most popular and simplest ways to do this is creating a spreadsheet using Ms Excel and use Risk Solver, a simulation tool by Frontline Systems.
Other things required to use the Monte Carlo method or ways to implement this concept are writing code in a programming language, such as C++, Java, C# or Visual Basic. You can also use a special simulation modeling language.
Not just these, you also need to have a basic knowledge of statistics and probability. To successfully resolve the uncertainties in the complex model in hand, you need to replace some fixed numbers, say the spreadsheet cells with functions that use random samples from probability distributions. Where do you need statistics? In an analysis of the results you get from the simulation run, you will need statistics such as standard deviation, mean and percentiles as well as graphs and charts.
Role of Monte Carlo simulation in your work or career
As aforesaid, Monte Carlo simulation can be of great use in a diverse range of problem areas and if your work is related to any of those fields, you are on the gainer’s end. What we mean to say is if your success is directly proportional to the forecasts or activities that involve uncertainties, you have a great chance of getting the advantage of learning the Monte Carlo method.
Here are a few ways you can benefit from the method in your career.
You go ‘off-limits’ in case of the ‘What If’ analysis
You can only do it using a traditional spreadsheet model. Suppose you have made different models with the best case, average case and worst-case scenarios, only to see that the actual outcome was way too different than what you thought, you need to learn Monte Carlo method. Using the ‘What If’analysis by exploring thousands of combinations and considering the complete range of possible outcomes, you can have better results in terms of accuracy, with just a little additional effort.
Understand what factors actually matter
There are certain tools that allow you to easily identify the major impact factors in the concerned model. You can use sensitivity analysis across several Monte Carlo trials. It may take hours to know these factors using the conventional ‘What If’ method.
Take a competitive benefit
In case you are into a negotiation of a deal or just competing in the market, Monte Carlo can be of great help. You can have a realistic idea of the different outcomes with probability distributions, while your competitor has no idea of doing this. You can allow yourself to get a better bargain, fix a price that brings you more profit or enjoy other kinds of benefits.
Get prepared for executive decisions
Monte Carlo method helps in decision making and as you reach a higher position in an organization, the more you deal with uncertainties. Risk analysis or simulation can be of great help in dealing with more strategic, higher-level or higher-stakes decisions.
Use of Monte Carlo simulation in different applications
Let’s now discuss the various applications in which Monte Carlo simulation can help find a solution or contribute in making a decision.
The example of rolling dice
We would like to start with the most simple example of the Monte Carlo method – rolling dice.
Consider calculating the probability of a specific sum of throwing two dice, with each die being numbered from one to six. In this case, there are 26 combinations of the dice rolls.
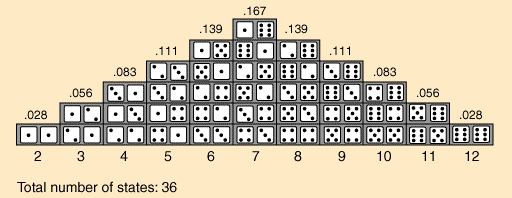
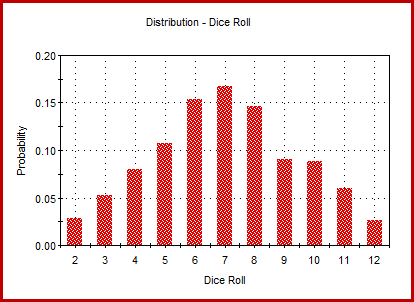
Based on this combination, you can now manually calculate the probability of a specific outcome. Consider an example – there are six ways in which the dice could get the number seven (sum of both the die). This way, the probability of rolling seven is equal to six divided by thirty-six, which is 0.167.
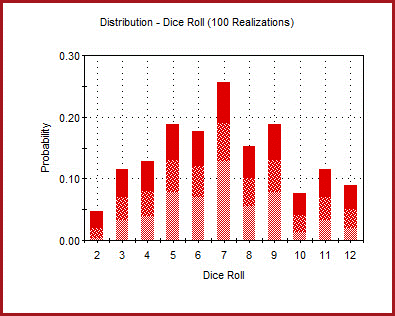
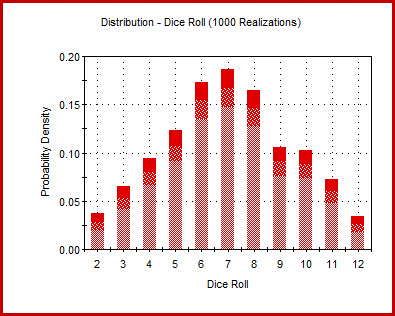
Now we have a different way to get more accurate results. You can roll the dice 100 times and note how many times each outcome occurs. If the dice sums to seven 18 times out of the 100 rolls, the probability of rolling seven is approximately 18% or 0.18 times. The more you roll the dice, the less approximate the result would get. Instead of rolling the dice 100 times manually, you can use a computer to simulate the rolling of the dice 10,000 times or even more. As we know the probability of a specific outcome for one die, it gets simple. The output of around 10,000 dice rolls using a software:
Accuracy of the results
The accuracy of the results using the Monte Carlo method is a function of the total number of realizations. It indicates that the correctness of the results can be easily calculated or computed based on the total number of realizations.
The examples given below show that 95% and 5% confidence bounds on the value of each result. So, it shows a chance of 90% that the exact value is between the confidence bounds.
Estimation of Pi using Monte Carlo Method
We all have learned in geometry that pi is a constant that signifies the ratio of the circumference to the diameter of a circle. The value of pi is an irrational number, that is, the value has infinite digits without any definite pattern.
How about if we say that you can estimate the value of pi to as many digits as you want by just playing a game of cards? Would you believe us? Well, you will after knowing about this example.
As it is a game of chance, you can get an estimate to a particular degree of uncertainty.
Let us refer to the below python script to know how:

In the above script or code, we have generated random points within a box and have counted the total number of points that fall within the boundary of an embedded circle.
To make it simpler for you, we will focus only on the upper quadrant of the dartboard which is of a radius R and is fixed on a square wooden block, having the same width.
Now, if you throw 100 darts and count the number of darts hitting the dartboard successfully, we may see something like the below picture:
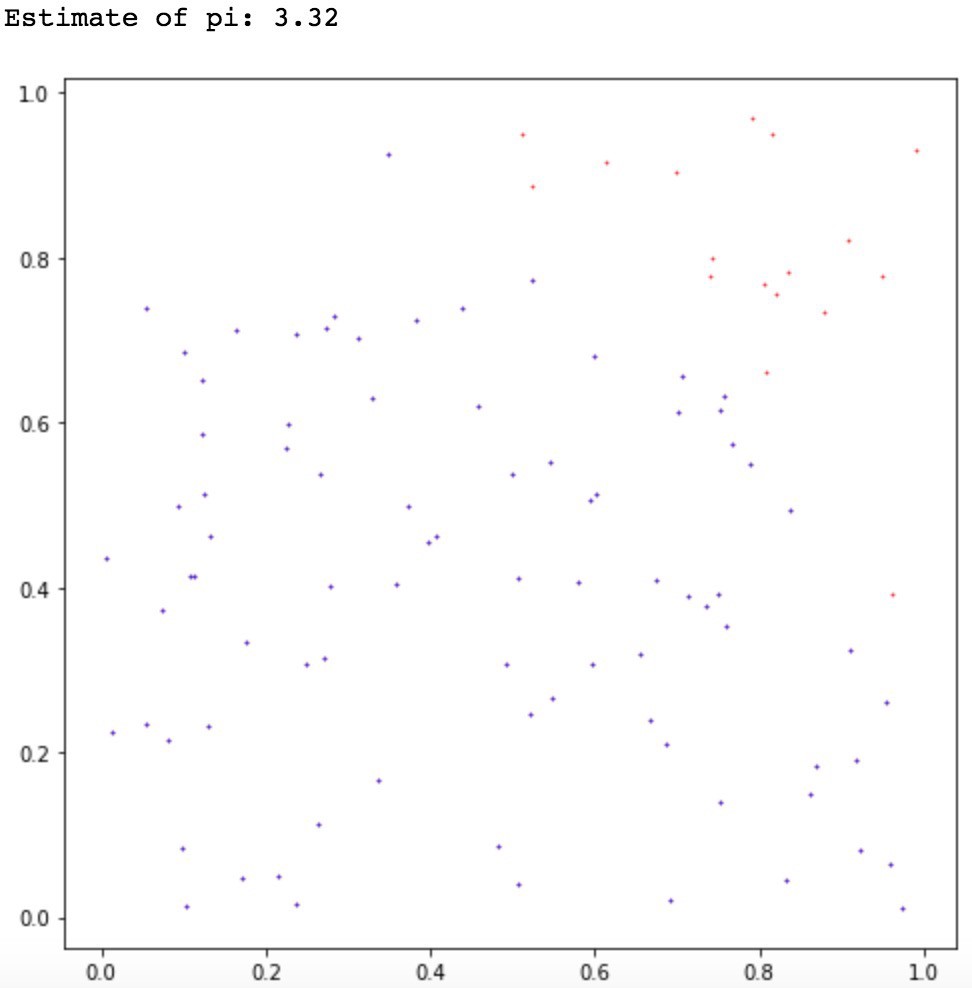
If you just thought ‘Why are we so bad doing this?’, you have the right question on your mind. In this example, the location of the darts must be uniformly distributed all over the area, so we will not be winning games here definitely.
Fro this setup, the probability of hitting the board with darts will be π/4. As we continue the game and as n approaches to ∞, we also approach the true value of pi.
You can see the same as we increase n by an order of ten:
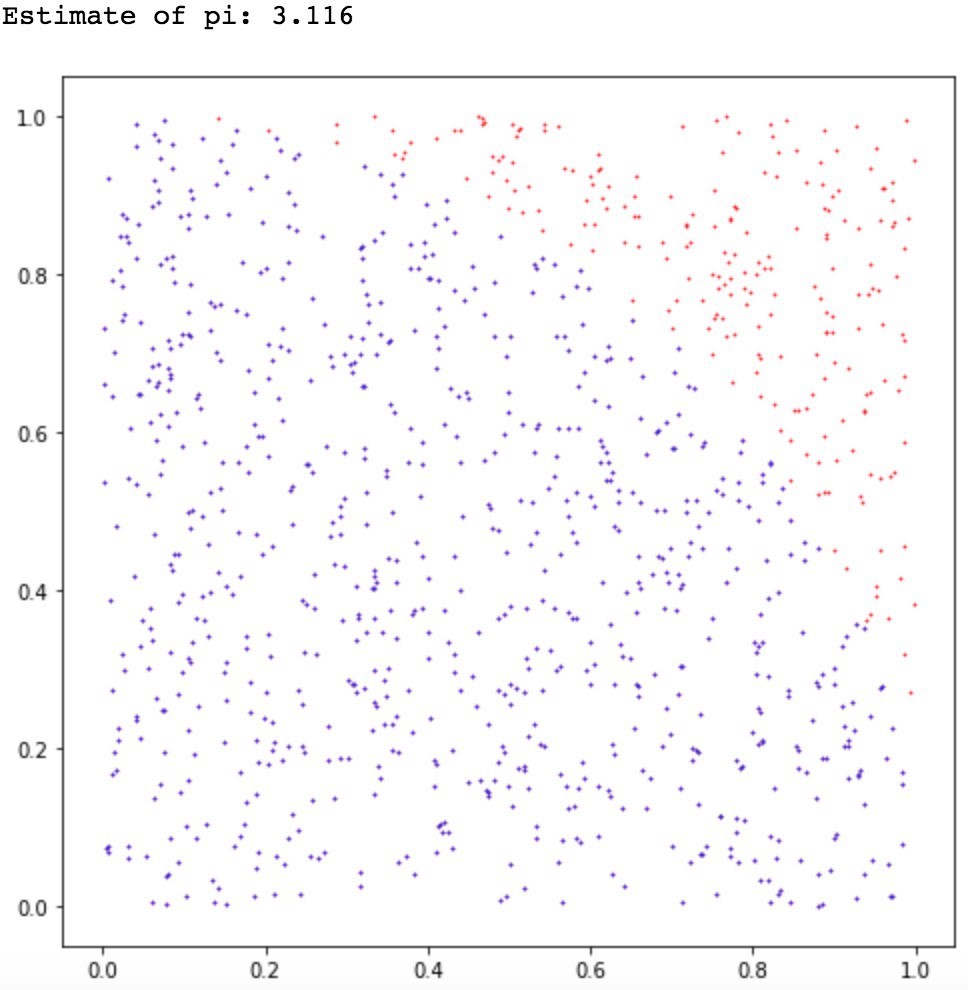
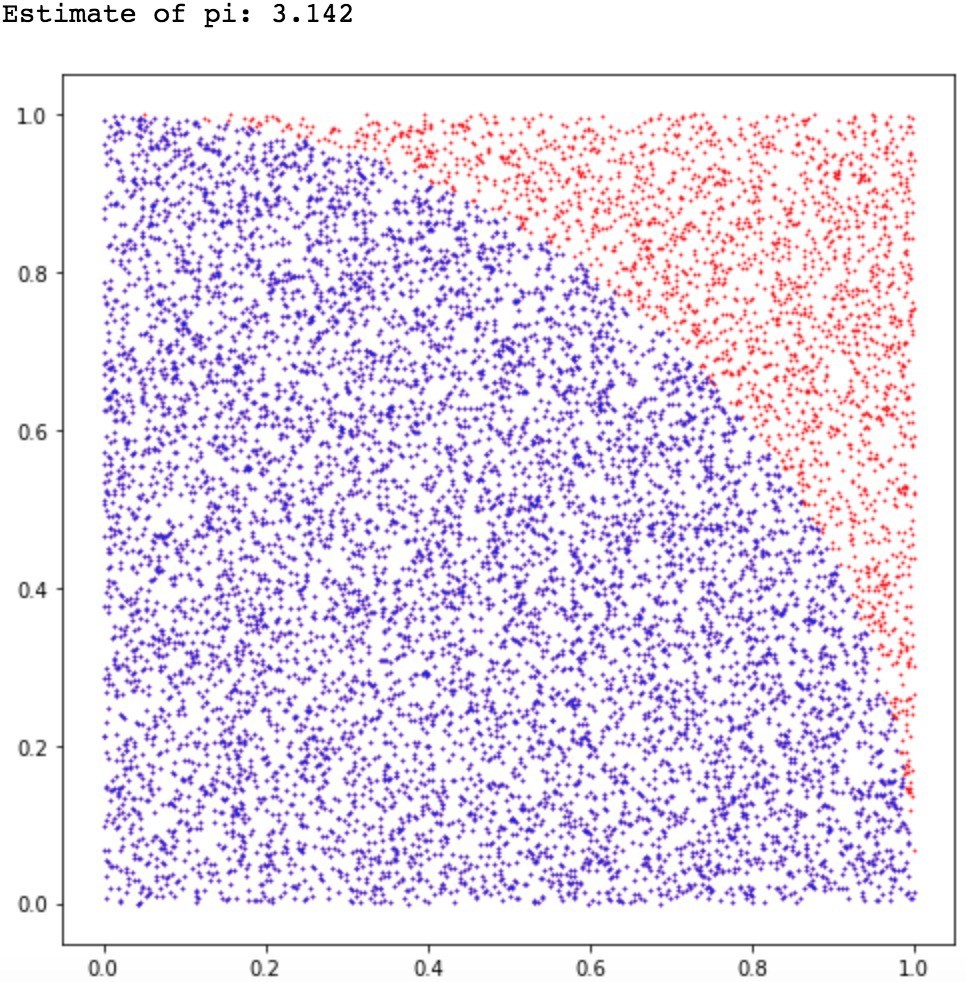
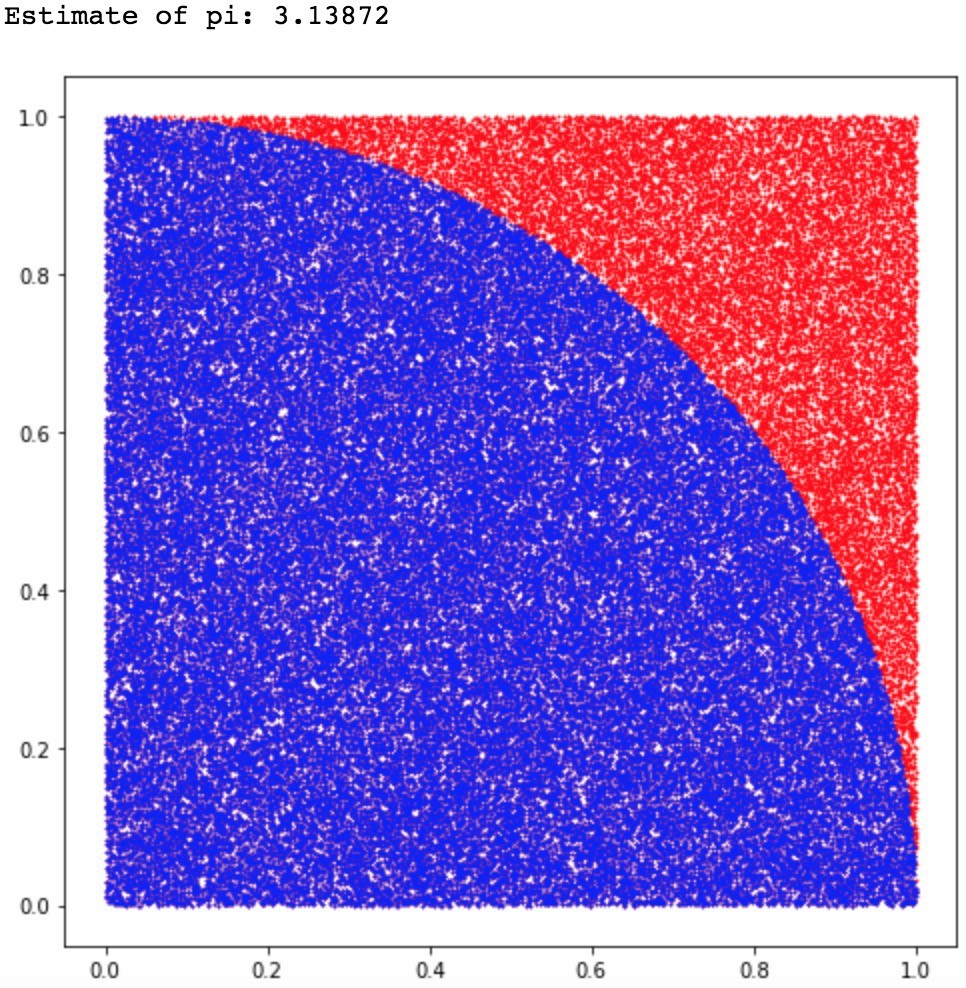
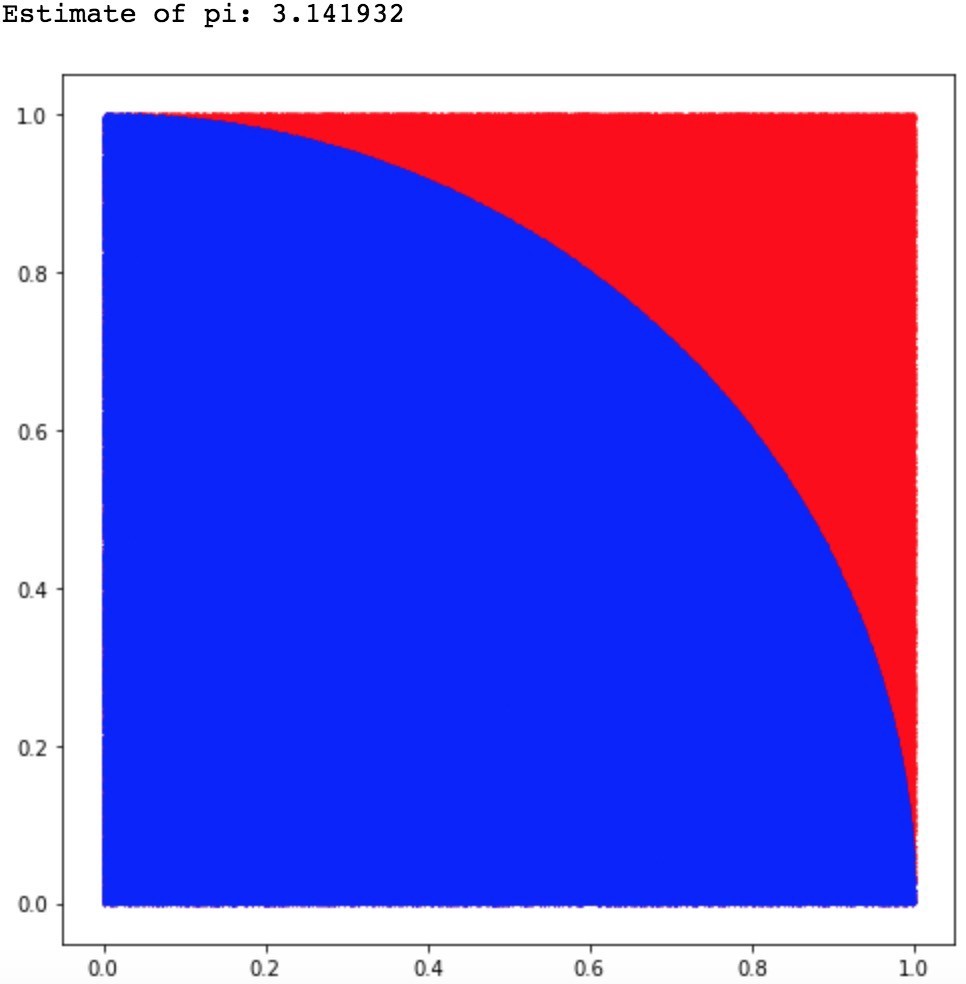
Plots for n= one, ten, and one-hundred-thousand, and finally one million points.
At this point, you might be thinking that I already know the value of pi, it is 3.14159. And, anyway what is uniformly distributed in the real world?
We understand you. But, you need not worry about this when using the MC methods for higher-dimensional systems. In a situation like that, you need to sample all kinds of random variables considering different probability distributions that represent the more accurate results in the model.
Monte Carlo in high-energy Physics
Another significant application of MC (Monte Carlo) simulation is in the world of particle physics. So, what happens in the quantum world is that things are not very easily observable. Consider a point of collision in a particle accelerator. To run simulations of such events, physicists use MC methods, based on the parameters and Standard Model that have been observed/identified from the experiments performed earlier.
Monte Carlo simulation in the finance field
If the applications described above doesn’t connect to you or you do not find these exciting, what if we say MC simulation is used in financial engineering for the stock market forecast? Yes, that is true!
It is used in the stock market as it is impossibly difficult to model, has a lot of data to sample and has extremely high dimensionality. Another reason why financial analysts use Monte Carlo simulation in the stock market forecast is that the importance of risk is a large factor to consider. One of the ways to apply MC method in the finance field is portfolio optimization.
Without going into much detail, we will try explaining to you the concept of portfolio optimization. You choose a [portfolio of stocks and work on the different levels of risk based on your objectives and financial goals. By using Monte Carlo methods, you can maximize your returns per volatility of the chosen portfolio without worrying about the risks. MC methods help you find the proportions of stocks and the optimal combinations.
You can also use historical data to generate hundreds of different combinations of stocks in various ratios. This way, you can see how each combination would perform during that particular period of time. Now, that’s interesting!
In a Nutshell
Monte Carlo simulation is a computer technique that works using probability distributions of the most possible outcome of a decision you need to make. Not just decisions, it helps in a process where you need to forecast, estimate or assess any kind of risk quantitatively.
Now that you know about the history, use and purpose of the Monte Carlo methods, you can apply it to various relative fields. Are you into the stock market? MC methods can be of great help in maximizing the returns!

